울타리 잘라내기

• 1. Problem
• 2. My Approach
• 3. Implementation
• 4. Textbook Approach
• 5. Implementation
• 6. Analysis
• 7. Feedback

1. Problem

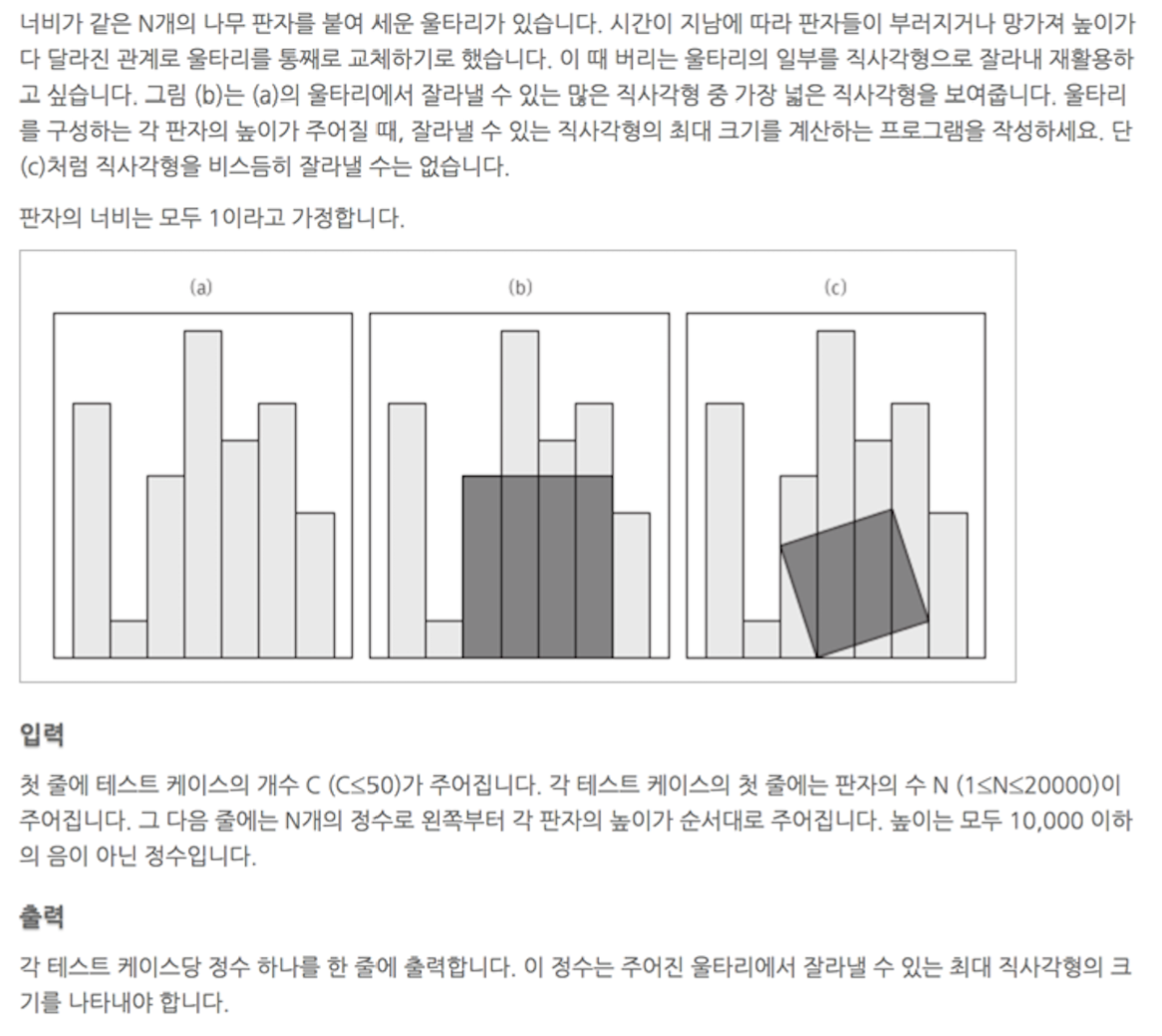
2. My Approach

• 처음 시작 인덱스의 울타리와 나머지 울타리들로 나누는 분할 정복을 사용하는 재귀함수를 구현하려 했으나 그 동작하는 알고리즘을 생각할 수 없었다.
• 그래서 그냥 단순하게 반복문을 통해 모든 경우의 수를 세어 보기로 했다.
• 첫 번째 위치한 울타리(i)를 포함한다고 가정하고 나머지 울타리들을 하나씩 추가하면서 비교한다.
• 첫 번째 위치한 울타리를 제외한다고 가정하고 두 번째(i+1)부터 위 과정을 반복한다.
• 직사각형의 너비 = 선택된 울타리 개수 * 그 것 들 중 가장 낮은 울타리 높이

3. Implementation

• 주어지는 울타리들의 높이를 저장하는 fences[ ] 선언
• fences[start]를 포함한다고 가정하고 마지막 울타리까지 하나씩 추가해주면서 만들어지는 직사각형 중 가장 큰 값을 구한다.
• start 인덱스를 하나씩 증가시켜주면서 위의 두 연산을 반복하면서 가장 큰 직사각형의 너비를 반환한다.

int largest=0;
for(int l=0; l<fences.size(); l++){
    int height = fences.at(l);
    for(int r=l; r<fences.size(); r++){
        height = min(height, fences.at(r));
        largest = max(largest, height*(r-l+1));
    }
}

• 당연히 시간초과가 발생한다..

4. Textbook Approach

• 본인이 시작인덱스와 나머지로 분할하려는 것과 달리 책은 중간을 기준으로 왼쪽과 오른쪽으로 분할하는 것으로 접근했다.
• 중간으로 나눠진 왼쪽과 오른쪽은 각각 재귀적으로 분할되면서 한개의 울타리만을 형성할 때까지 도달한 뒤, 크기를 비교하며 크기가 큰 직사각형 너비를 반환하며 정복된다.
• 여기서 요점은 가장 큰 너비를 형성하는 직사각형이 위치하는 경우를 세가지로 나누어 비교한다.

  1. 중간 울타리 기준 왼쪽에 위치
  2. 중간 울타리 기준 오른쪽에 위치
  3. 중간 울타리 포함하여 위치

• 재귀 함수 내에서 이 세 가지의 경우를 어떻게 구하고 비교하는 지 주목하자.

5. Implementation

int findLarggest(int left, int right){
    //  base case
    if(left == right)
        return fences[left];
    //  In the case that the largest is a fence
    int mid = (left+right)/2;

    //  Moving the pointers to the left or the right from the mid,
    //  compare which combination is larger than the other
    //  (compare which height of the directions is larger than the other)
    int larggest = max(findLarggest(left, mid), findLarggest(mid+1, right));

    larggest = max(larggest, 2*min(fences[mid], fences[mid+1]));

    int l = mid; int r = mid+1;
    int height = min(fences[l], fences[r]);
    while(r<right || l>left){
        // In the case that the left fence is larger than the opposite one
        // 왼쪽 있어야하고 && (오른쪽이 끝났거나, 왼쪽 다음이 오른쪽 다음보다 커야함)
        if(l>left && (r==right || fences[l-1]>fences[r+1])){
            l--;
            height = min(height, fences[l]);
        }
        else{
            r++;
            height = min(height, fences[r]);
        }

        larggest = max(larggest, height*(r-l+1));
    }
    return larggest;
}

6. Analysis

• findLarggest()는 n크기의 배열을 n/2크기의 배열로 나눈 뒤 이들을 재귀적으로 호출한다.
• 함수 내에서 시간을 소요하는 부분은 가운데 울타리를 포함하는, 즉 걸쳐있는 직사각형을 찾는 작업밖에 없으므로, 이 작업의 시간 복잡도가 전체 시간 복잡도를 결정한다.
• 함수 내의 while문은 너비가 n인 사각형까지 접근하므로 O(n)의 시간복잡도를 갖는다.
• 결국에 문제를 항상 절반으로 나누어서 재귀 호출하고, O(n) 시간의 후처리를 하는 알고리즘인데, 이는 병합 정렬(Merge Sort)과도 같다. 따라서 이 분할 정복 알고리즘도 병합 정렬과 같은 시간 복잡도 O(nlgn)을 갖는다.

7. Feedback

• 단순히 재귀함수와 분할-정복 구조를 통해 문제를 해결하는 매커니즘을 생각할 수 있는 것 외에도 얼마나 많은 시간을 절약할 수 있는 지 느낄 수 있다.
• 본 문제 외에 재귀함수를 사용하는 몇 개의 문제를 풀어본 결과, 재귀함수의 구현은 분할 정복과 관련하여 몇가지 유형으로 나누어 접근할 수 있음을 느꼈다.

  1. 기저 사례(base case)는 주어진 범위의 끝 ‘무렵’에 도달했을 경우(start 또는 end)
  2. input의 처음과 나머지로 나누어 접근 또는 가운데를 기준으로 나누어 접근