Heeveloper

고대어 사전

2017-07-19
Heeveloper
Algorithm
             

1. Problem

screenshot

2. My Approach

  • 문자들은 이미 임의의 사전 순서대로 입력 되어진다.
  • 따라서 이전에 입력된 문자(first)와 현재 입력된 문자(second)간의 비교를 통해 정렬된 배열에 넣어주고 기존의 알파벳 순으로 저장되어 있던 배열에선 해당 문자들을 빼준다. 위의 연산은 기존의 알파벳순에 역행하는 경우에만 처리해준다.
  • 정렬된 배열에 넣기 전에 배열 안의 해당 값들의 존재 여부에 따라 다르게 처리한다.
    • 둘 다 없을 경우, first-second 순으로 넣는다.
    • first만 있는 경우, 해당 first 인덱스+1 위치에 second 넣는다.
    • second만 있는 경우, 해당 second 인덱스 위치에 first 넣는다.
    • 만일 둘 다 있지만 넣으려고 하는 순서(first-second)에 위배되어 위치하고 있을 경우, 이는 모순이므로 예외값(-1)을 넣는다.
  • 그러나 이 방법은 세 단어 이상의 상관관계에 있어서 허용가능한 상황을 모순으로 처리할 수 있어 결국에 모순이 발생한다.
  • 그래프의 특성을 이용하지 않아, 결국엔 복잡할 뿐만 아니라 예상하지 못한 예외상황을 발생시켰다. 아래 코드는 대충 참고하고 책의 접근 방법을 알아보자.

3. Implementation

while(N--){
            p=0;
            cin >> second;
            while(first[p]==second[p])
                p++;

            vector<int>::iterator it = find(ordered.begin(), ordered.end(), first[p]);
            vector<int>::iterator it2 = find(ordered.begin(), ordered.end(), second[p]);

            if(it == ordered.end() && it2 == ordered.end()){
                ordered.push_back(first[p]);
                ordered.push_back(second[p]);
                if(find(alphabet.begin(), alphabet.end(), first[p]) != alphabet.end())
                    alphabet.erase(find(alphabet.begin(), alphabet.end(), first[p]));
                if(find(alphabet.begin(), alphabet.end(), second[p]) != alphabet.end())
                    alphabet.erase(find(alphabet.begin(), alphabet.end(), second[p]));
            }
            else if(it == ordered.end()){
                ordered.insert(it2, first[p]);
                if(find(alphabet.begin(),alphabet.end(), first[p]) != alphabet.end())
                    alphabet.erase(find(alphabet.begin(),alphabet.end(), first[p]));
            }
            else if(it2 == ordered.end()){
                ordered.push_back(second[p]);
                //ordered.insert(it+1, second[p]);
                if(find(alphabet.begin(), alphabet.end(), second[p]) != alphabet.end())
                    alphabet.erase(find(alphabet.begin(), alphabet.end(), second[p]));
            }
            else if(it > it2){
                ordered.push_back(-1);
            }
            first = second;
        }

4. Textbook Approach

  • 그래프로 나타내려는 문자 간에는 우선순위가 존재하기 때문에 이를 간선을 의미하는 인접행렬의 해당 행과 열에 표시를 해주어 그래프를 완성시킨다.(makeGraph)
  • 깊이우선탐색을 통해 주어진 인자와 연결된 인자에 재귀함수를 통해 우선적으로 접근한 뒤, 끝에 도달했을 때 해당 값을 정렬된 값을 저장하는 배열에 저장한다.(dfs)
  • 탐색을 거친 인자는 따로 표시를 해두어 중복 접근을 막는다.
  • 위상정렬을 통해 순서대로 모든 인자에 깊이우선탐색을 적용한다.

5. Implementation

#include <iostream>
#include <vector>

using namespace std;

vector<vector<int>> adj;
vector<int> seen, order;

void makeGraph(const vector<string>& words){
    adj = vector<vector<int>>(26, vector<int>(26,0));
    for(int j=1;j<words.size();j++){
        int i=j-1, len = min(words[i].size(), words[j].size());
        //word[j]가 word[i] 앞에 오는 이유를 찾는다.
        for(int k=0;k<len;k++)
            if(words[i][k] != words[j][k]){
                int a = words[i][k] - 'a';
                int b = words[j][k] - 'a';
                adj[a][b] = 1;
                break;
            }
    }
}

void dfs(int here){
    seen[here] = 1;
    for(int there=0;there<adj.size();there++)
        if(adj[here][there] && !seen[there])
            dfs(there);
    order.push_back(here);
}

//adj에 주어진 그래프를 위상정렬한 결과를 반환한다.
//그래프가 DAG가 아니라면 빈 벡터를 반환한다.
vector<int> topologicalSort(){
    int n = adj.size();
    seen = vector<int>(n,0);
    order.clear();
    for(int i=0;i<n;i++)
        if(!seen[i]) dfs(i);
    reverse(order.begin(), order.end());

    //만약 그래프가 DAG가 아니라면 정렬 결과에 역방향 간선이 있다.
    for(int i=0;i<n;i++)
        for(int j=i+1;j<n;j++)
            if(adj[order[j]][order[i]])
                return vector<int>();
    //없는 경우라면 깊이 우선 탐색에서 얻은 순서를 반환한다.
    return order;
}

int main( ) {
    int T;
    cin >> T;
    while(T--){
        int N;
        cin >> N;
        vector<string> words = vector<string>(N);
        for(int i=0;i<N;i++)
            cin >> words[i];
        makeGraph(words);
        vector<int> result = topologicalSort();
        if(result.empty())
            cout << "INVALID HYPOTHESIS" << endl;
        else{
            for(int i=0;i<result.size();i++)
                cout<<(char)(result[i]+'a');
            cout<<endl;
        }
    }
    return 0;
}

6. Analysis

깊이 우선 탐색(Depth-First Search;DFS)

깊이 우선 탐색의 시간복잡도는 어떤 그래프 표현 방식을 사용하느냐에 따라 달라진다.

  • 인접 리스트 사용
    • dfs( )는 한 정점마다 한 번씩 호출되므로, 정확히 |V|번 호출된다.
    • dfs( ) 한 번의 수행 시간은 모든 인접 간선을 검사하는 for문에 의해 지배되는데, 모든 정점에 대해 dfs( )를 수행하고 나면 모든 간선을 정확히 한 번(방향 그래프의 경우) 혹은 두 번(무향 그래프의 경우)확인함을 알 수 있다.
    • 따라서 깊이 우선 탐색 시간 복잡도는 O(|V|+|E|)가 된다.
  • 인접 행렬 사용
    • 마찬가지로 dfs( )의 호출 횟수는 그대로 |V|번이다.
    • 하지만 dfs( ) 내부에서 다른 모든 정점을 순회하며 두 정점 사이의 간선이 있는 가를 확인해야 하기 때문에 한 번의 실행에 O(|V|)의 시간이 든다.
    • 따라서 전체 시간 복잡도는 O(|V|^2)이 된다.

7. Feedback

위상 정렬(Topological Sort)
김치찌개 레시피와 같이 의존성이 있는 작업들이 주어질 때, 이들을 어떤 순서로 수행해야 하는지 계산해 준다.
각 작업을 정점으로 표현하고, 작업 간의 의존 관계를 간선으로 표현한 방향 그래프를 의존성 그래프(Dependency Graph)라고 한다.

  • 의존성 그래프

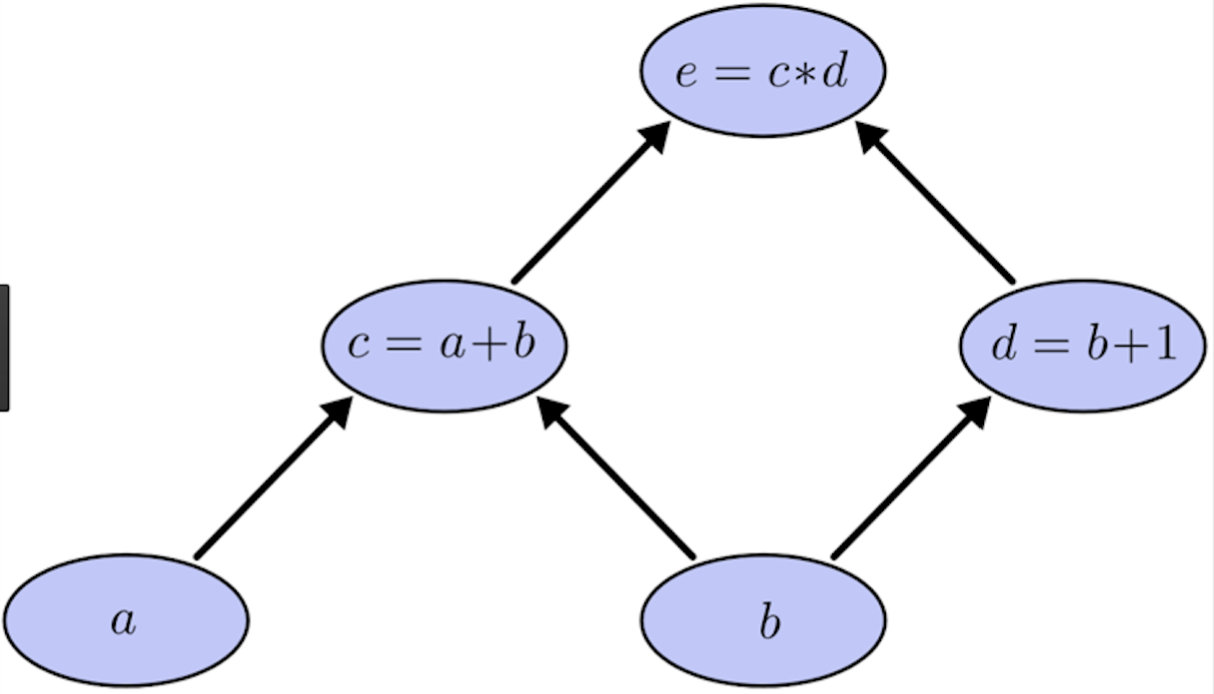
    screenshot

의존성 그래프는 사이클 없는 방향 그래프(Directed acyclic graph; DAG)다.
위상 정렬을 구현하는 가장 직관적인 방법은 들어오는 간선이 하나도 없는 정점들을 하나씩 찾아서 정렬 결과를 뒤에 붙이고, 그래프에서 이 정점을 지우는 과정을 반복하는 것이다. 적절한 자료구조를 사용하면 이런 알고리즘도 효율적으로 구현할 수 있지만, 깊이 우선 탐색을 이용하면 더 간단하게 이 문제를 해결할 수 있다.

  • dfsAll( ) 
    void dfsAll(){
   //  visited를 모두 false로 초기화한다.
   visited = vector<bool>(adj.size(), false);
   //  모든 정점을 순회하면서, 아직 방문한 적 없으면 방문한다.
   for(int i=0;i<adj.size();i++)
       if(!visited[i])
           dfs(i);
}

    dfsAll( )을 수행하며 dfs( )가 종료할 때마다 현재 정점의 번호를 기록한다.
    dfsAll( )이 종료한 뒤 기록된 순서를 뒤집으면 위상 정렬 결과를 얻을 수 있다.
    따라서 dfs( )가 늦게 종료한 정점일수록 정렬 결과의 앞에 온다.



인자 간의 연결 요소, 상하관계 등이 보이면 주어진 문제를 그래프로 시각화하여 접근한다.
이 때 만들어진 그래프의 원하는 의미를 도출하기 위해 다양한 접근 방법과 알고리즘을 익혀둘 필요가 있다.

prev 연습시즌

next 단어 제한 끝말잇기

Comments

Content
-->