Heeveloper

하노이의 탑

2017-07-23
Heeveloper
Algorithm
           

1. Problem

screenshot

2. My Approach

  • 4개의 stack을 생성해 각각에 원반을 위치시킨다.
  • bfs 를 통해 다음의 과정을 반복한다.

    각각의 원반의 위치를 검사하고, 목표값과 다를 시에 가장 위에 위치한 임의의 원반을 임의의 기둥으로 옮긴다. 원반을 한번 옮겼을 때 발생하는 경우의 수를 모두 계산한 뒤, 그 중에 없으면 이 경우들에서 한 번 더 옮겨 반복한다.

3. Implementation

  • 두 개의 큐를 선언한다.
    1. toCheck : 목표값과 같은 지 검사해야할 값들 저장.
    2. toMove : 검사결과 목표값이 아니어서 위치를 옮겨야 될 값들 저장.
  • 이 전에 푼 SortGame과 같은 실수를 저질렀다. 수행시간뿐만 아니라 메모리도 기하급수적으로 늘어난다.
//
//  main.cpp
//  HANOI4
//
//  Created by  Heejun Lee on 7/25/17.
//  Copyright © 2017  Heejun Lee. All rights reserved.
//

#include <iostream>
#include <stack>
#include <queue>

using namespace std;

struct Hanoi {
    stack<int> sticks[4];
    int count;
};

int T,N;
queue<Hanoi> toCheck;
queue<Hanoi> toMove;

int move(Hanoi hanoi){
    toCheck.push(hanoi);
    while(1){
        while(!toCheck.empty()){

            cout << "Count:" << toCheck.front().count << endl;
            cout << toCheck.front().sticks[0].size() << " " <<toCheck.front().sticks[1].size() << " "<<toCheck.front().sticks[2].size() << " "<< toCheck.front().sticks[3].size() << endl;

            if(toCheck.front().sticks[3].size() == N) return toCheck.front().count;
            toMove.push(toCheck.front()); toCheck.pop();
        }
        while(!toMove.empty()){
            for(int from=0;from<4;from++)
                for(int to=0;to<4;to++)
                    if(from!=to)
                        if(!toMove.front().sticks[from].empty())
                            if(toMove.front().sticks[to].empty() || toMove.front().sticks[from].top() < toMove.front().sticks[to].top()){
                                toMove.front().sticks[to].push(toMove.front().sticks[from].top()); toMove.front().sticks[from].pop();
                                toMove.front().count++;
                                toCheck.push(toMove.front());
                                toMove.front().count--;
                                toMove.front().sticks[from].push(toMove.front().sticks[to].top()); toMove.front().sticks[to].pop();
                        }
            toMove.pop();
        }
    }
}

int main() {
    cin >> T;
    while(T--){
        Hanoi hanoi;
        hanoi.count=0;
        cin >> N;
        for(int i=0;i<4;i++){
            int nums;
            cin >> nums;
            while(nums--){
                int num;
                cin >> num;
                hanoi.sticks[i].push(num);
            }
        }
        cout << move(hanoi) << endl;
        while(!toMove.empty()) toMove.pop();
        while(!toCheck.empty()) toCheck.pop();
    }
    return 0;
}
  • 시간 초과 이전에 메모리 초과로 Runtime Error가 발생한다.
  • 주어진 상황을 의미하는 4개의 stack은 bfs로 다루기에 사이즈가 너무 크다.

    이전의 SortGame 에선 이를 극복하기 위해 map을 사용했지만 본 문제는 기둥의 관점이 아니라 원반의 관점에서 봤을 때, 각각 1~4의 값을 가지므로 이는 2bit만으로도 표현이 가능하다. 따라서 map 대신에 Bitmask를 적용할 수 있다.

4. Textbook Approach

두가지의 풀이가 주어진다.

  1. 본인의 코드와 비슷하지만 단일 Queue와 Bitmask를 사용하여 메모리가 커지는 것은 막았지만 시간 초과는 여전히 일어난다.
  2. 시작 상태와 마지막 상태를 알고 있으므로 양방향에서 접근하도록 구현하였다.

5. Implementation

1. 단일 큐와 Bitmap 사용 알고리즘

  • 별도로 get( )과 set( ) 함수를 만들어 좀 더 편하게 Bitmask를 이용할 수 있게 하였다.
  • 각각의 상황이 되기까지의 뒤집은 횟수를 저장하는 cache역할을 하는 배열도 Bitmask로 구현하였다.

    처음 방문하지 않은 상태의 뒤집은 횟수는 -1로 초기화한다.

#include <iostream>
#include <queue>
#include <cstring>

using namespace std;

int T, N;
const int MAX_PAN = 12;
int c[1<<(MAX_PAN*2)];

//  index : 원반 번호
//  value : 막대기 번호
int get(int state, int index){
    return (state >> (index*2)) & 3;
}

int set(int state, int index, int value){
    return (state & ~(3<<(index*2))) | (value << (index*2));
}

int bfs(int discs, int begin, int end){
    if(begin == end) return 0;
    queue<int> q;
    memset(c, -1, sizeof(c));
    q.push(begin);
    c[begin]=0;
    while(!q.empty()){
        int here = q.front();
        q.pop();
        int top[4] = {-1,-1,-1,-1};
        for(int i=discs-1;i>=0;--i)
            top[get(here,i)]=i;
        //  i번 기둥의 맨 윗 값을 j번 기둥으로 옮긴다
        for(int i=0;i<4;++i)
            if(top[i] != -1)
                for(int j=0;j<4;j++)
                    if(i!=j && (top[j] == -1 || top[j]>top[i])){
                        int there = set(here,top[i],j);
                        if(c[there] != -1) continue;
                        c[there] = c[here] + 1;
                        if(there == end) return c[there];
                        q.push(there);
                    }
    }
    return -1;
}

int main() {
    cin >> T;
    while(T--){
        cin >> N;
        int num,n;
        int first=0;
        int end = pow(2, 2*N)-1;
        for(int i=0;i<4;i++){
            cin >> num;
            for(int j=0;j<num;j++){
                cin >> n;
                first = set(first,n-1,i);
            }
        }
        cout << bfs(N, first, end) << endl;
    }
    return 0;
}



2. 양방향 알고리즘

  • 기존의 bfs 알고리즘과 큰 차이는 없다.
  • 다만 정방향과 역방향을 구분하기 위해 각각 뒤집히는 갯수가 증가하는 개념을 양의 방향과 음의 방향으로 나누었다.
    • incr( ) : 방향에 맞게 1씩 증가시키는 함수
    • sgn( ) : 뒤집힌 갯수의 부호를 반환해서 어느 방향에서 접근한 건지 구분
    • 때문에 뒤집힌 갯수를 저장해 놓는 캐시는 -1이 아닌 0으로 초기화하고 양쪽의 시작점(begin과 end)에서의 값은 각각 1과 -1부터 시작한 뒤 마지막에 반환할 때 1을 빼준다.
  • 가운데서 만난 경우

    here로부터 접근한 there가 방문한 기록이 있고(c[there] != 0), c[there]의 부호와 c[here]의 부호가 다른 경우 이는 양방향에서 접근하던 두 진행이 만난 것을 의미한다. 따라서 이 두 경우를 더하는데, 처음 초기값을 0이 아닌 1 또는 -1로 했기 때문에 c[there]-1 과 c[here]의 합을 반환하는 것에 주의하자.

int sgn(int x){
    if(!x) return 0;
    return (x>0)?1:-1;
}

int incr(int x){
    if(x<0) return x-1;
    return x+1;
}

int bidir(int discs, int begin, int end){
    if(begin == end) return 0;
    queue<int> q;
    //  초기화를 0으로 하는데 주의
    memset(c, 0, sizeof(c));
    q.push(begin); c[begin]=1;
    q.push(end); c[end]=-1;
    while(!q.empty()){
        int here = q.front();
        q.pop();
        int top[4] = {-1,-1,-1,-1};
        for(int i=discs-1;i>=0;--i)
            top[get(here,i)]=i;
        //  i번 기둥의 맨 윗 값을 j번 기둥으로 옮긴다
        for(int i=0;i<4;++i)
            if(top[i] != -1)
                for(int j=0;j<4;j++)
                    if(i!=j && (top[j] == -1 || top[j]>top[i])){
                        int there = set(here,top[i],j);
                        //   아직 방문하지 않은 정점인 경우
                        if(c[there] == 0){
                            c[there] = incr(c[here]);
                            q.push(there);
                        }
                        //  가운데에서 만난 경우
                        else if(sgn(c[there]) != sgn(c[here]))
                            return abs(c[there]) + abs(c[here]) - 1;
                    }
    }
    return -1;
}

6. Analysis

  • 양방향 탐색의 코드를 보면 너비 우선 탐색과 크게 다르지 않은 것을 알 수 있다. 하지만 실제 방문하는 정점의 수는 크게 줄어들고, 실제 수행 시간도 열 배 가까이 감소하는 것을 확인할 수 있다.

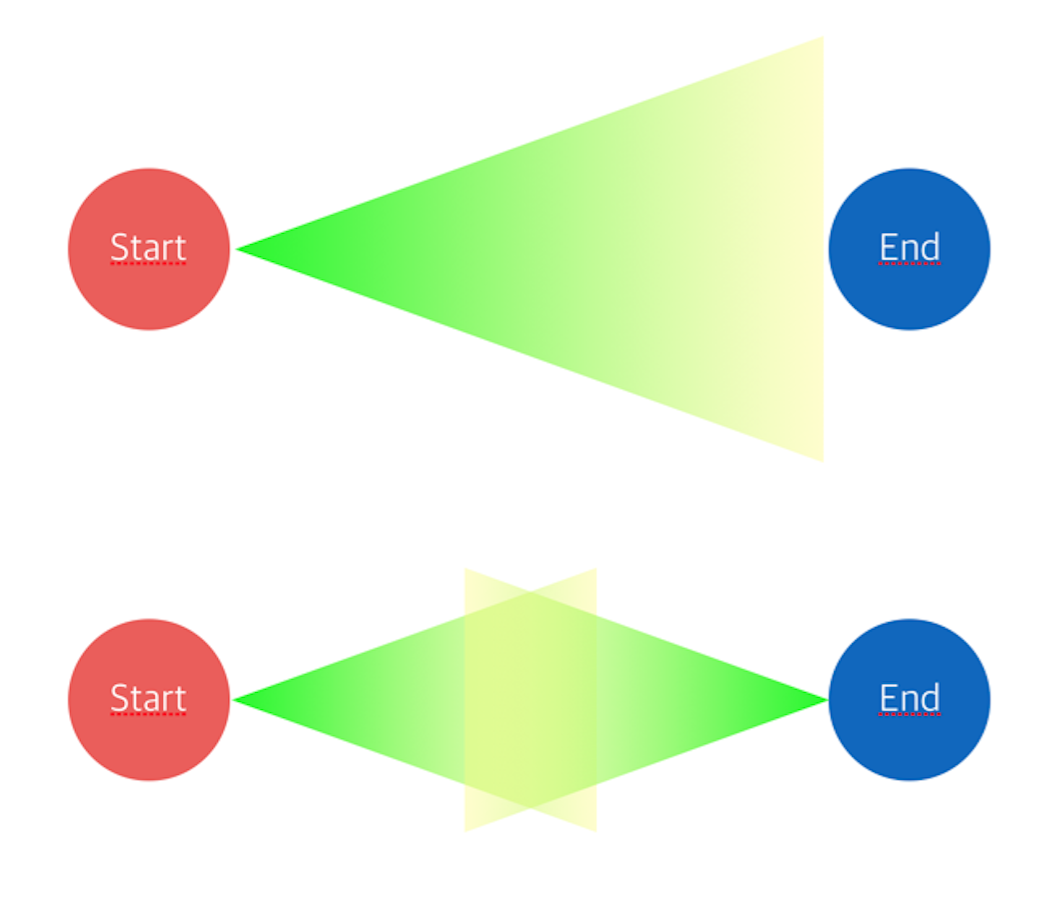
screenshot

7. Feedback

  • 메모리를 효율적으로 다루기 위해 Bitmap에 익숙해지자.
  • bfs의 또 다른 최적화 방법으로 양방향 접근이 가능하다는 것을 명심하자.

prev Sorting Game

next 징검다리

Comments

Content
-->