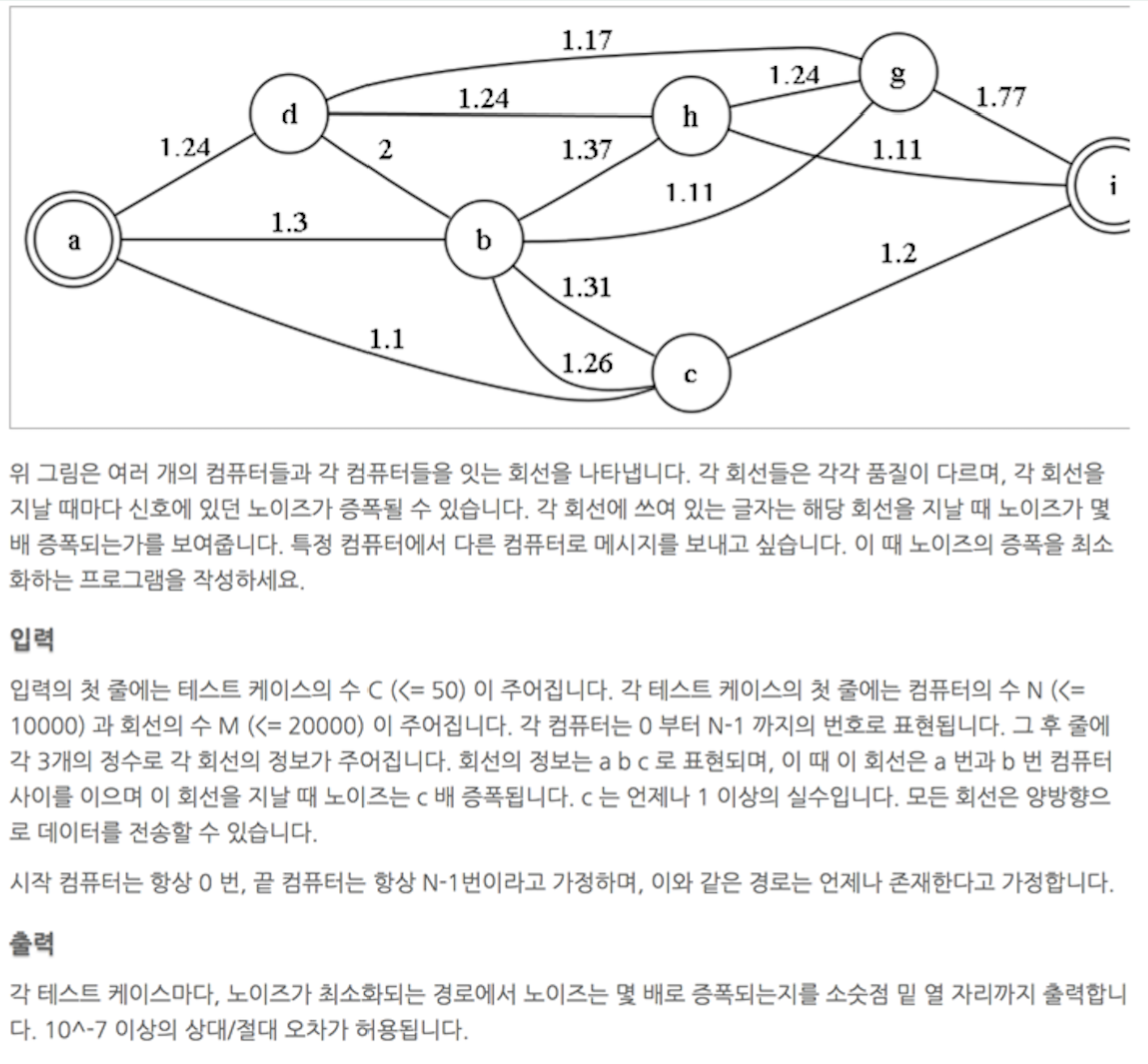
1. Problem
2. My Approach
- 최단 경로 알고리즘 중 다익스트라를 적용할 수 있는 기본적인 문제다.
- 본 문제에서의 최단 경로는 가중치들의 합이 아닌 곱이 최소가 되는 경로를 찾으면 된다.
- 기존의 다익스트라 알고리즘에서 약간만 수정해주면 된다.
3. Implementation
- 정점들간의 간선을 의미하는 인접리스트를 생성해준다.
- 시작점에서 각 정점들까지의 최단거리를 저장하는 배열을 생성한 뒤, 0.0으로 초기화한다.
- 시작점과 인접한 정점을 모두 구하여 정점이 작은 순서대로 우선순위 큐에 저장한다.
- (총거리, 정점번호)
- 최단거리를 구하기 위해선 정점까지의 거리가 최소인 것을 우선적으로 방문해야 하므로 우선순위 큐를 사용한다.
//
// main.cpp
// Routing
//
// Created by Heejun Lee on 7/28/17.
// Copyright © 2017 Heejun Lee. All rights reserved.
//
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
int T, V, E;
vector<vector<pair<int,double>>> adj; // <정점, 가중치>
double dijkstra() {
vector<double> dist(V+1, 0.0);
dist[0]=1.0;
priority_queue<pair<double, int>> PQ; // <가중치, 정점>
PQ.push(make_pair(-1.0, 0));
while(!PQ.empty()){
double cost = -PQ.top().first;
int here = PQ.top().second;
PQ.pop();
// 만약 지금 꺼낸 것보다 기존의 경로가 더 짧다면 지금 꺼낸 것을 무시한다.
if(dist[here] < cost) continue;
// 인접한 정점을 모두 조사한다.
for(int i=0;i<adj[here].size();i++){
int there = adj[here][i].first;
double thereDist = cost * adj[here][i].second;
// 더 짧은 경로를 발견하면, dist[]를 갱신하고 우선순위 큐에 넣는다.
if(dist[there] == 0.0 || dist[there] > thereDist){
dist[there] = thereDist;
PQ.push(make_pair(-dist[there], there));
}
}
}
return dist[V-1];
}
int main(int argc, const char * argv[]) {
cin >> T;
while(T--){
cin>>V>>E;
adj.clear();
adj.resize(V+1);
for(int i=0;i<E;i++){
int a,b;
double c;
cin >> a >> b >> c;
adj[a].push_back(make_pair(b,c));
adj[b].push_back(make_pair(a,c));
}
printf("%.10f\n",dijkstra());
}
return 0;
}
4. Analysis
- 다익스트라 알고리즘의 수행 시간은 크게 두 부분으로 나누어 볼 수 있다.
- 각 정점마다 인접한 간선들을 모두 검사하는 작업
- 우선순위 큐에 원소를 넣고 삭제하는 작업
-
각 정점은 정확히 한 번씩 방문되고, 따라서 모든 간선은 한 번씩 검사된다는 사실을 떠올리면, 간선들을 검사하는 데는 전체
O(|E|)의 시간이 걸린다. - 우선순위 큐에 원소를 넣고 삭제하는 데 드는 총 시간을 분석하기 위해선 우선순위 큐의 최대 크기가 얼마나 될 지 알아야 한다.
- 너비 우선 탐색에서는 모든 정점이 큐에 한 번씩만 들어가기 때문에 큐의 최대 크기는
O(|V|)이다. - 그러나 본 코드는 dist[ ]를 갱신할 때마다 원소를 우선순위 큐에 넣기 때문에 그 보다 많은 원소들이 들어갈 수 있다.
- 이러한 추가는 각 간선마다 최대 한 번 일어나기 때문에, 최대
O(|E|)개의 원소가 우선순위 큐에 저장될 수 있다. - 이 경우 우선순위 큐에 원소를 추가하거나 삭제하는 데는
O(lg|E|)의 시간이 걸리고, 따라서 전체 시간 복잡도는O(|E|lg|E|)가 된다.
- 너비 우선 탐색에서는 모든 정점이 큐에 한 번씩만 들어가기 때문에 큐의 최대 크기는
- 위 두 작업을 더하여
O(|E|+|E|lg|E|) = O(|E|lg|E|)가 된다. - 대게의 경우 그래프에서 간선의 개수
|E|는|V|^2보다 작기 때문에O(lg|E|) = O(lg|V|)이 된다. - 따라서 전체 시간 복잡도는
O(|E|lg|V|)가 된다.
5. Feedback
- Dijkstra Algorithm의 활용
- 이를 위한 동적 메모리 활용