프리랜서

1. Problem
2. My Approach
3. Implementation
4. Other Approach
5. Implementation
6. Feedback

1. Problem

SCPC 2회 예선문제 <프리랜서>
[Codeground Practice 참고](https://www.codeground.org/)

2. My Approach

만들어지는 모든 경우의 수를 전부 계산하여 그 중 최대값을 반환한다.
따라서 동적계획법을 떠올렸고, 다음과 같이 재귀함수를 구현한다.
- 첫 째주엔 P사뿐만 아니라 Q사의 일도 다 바로 처리되므로 특별하게(예외로) 처리한다.
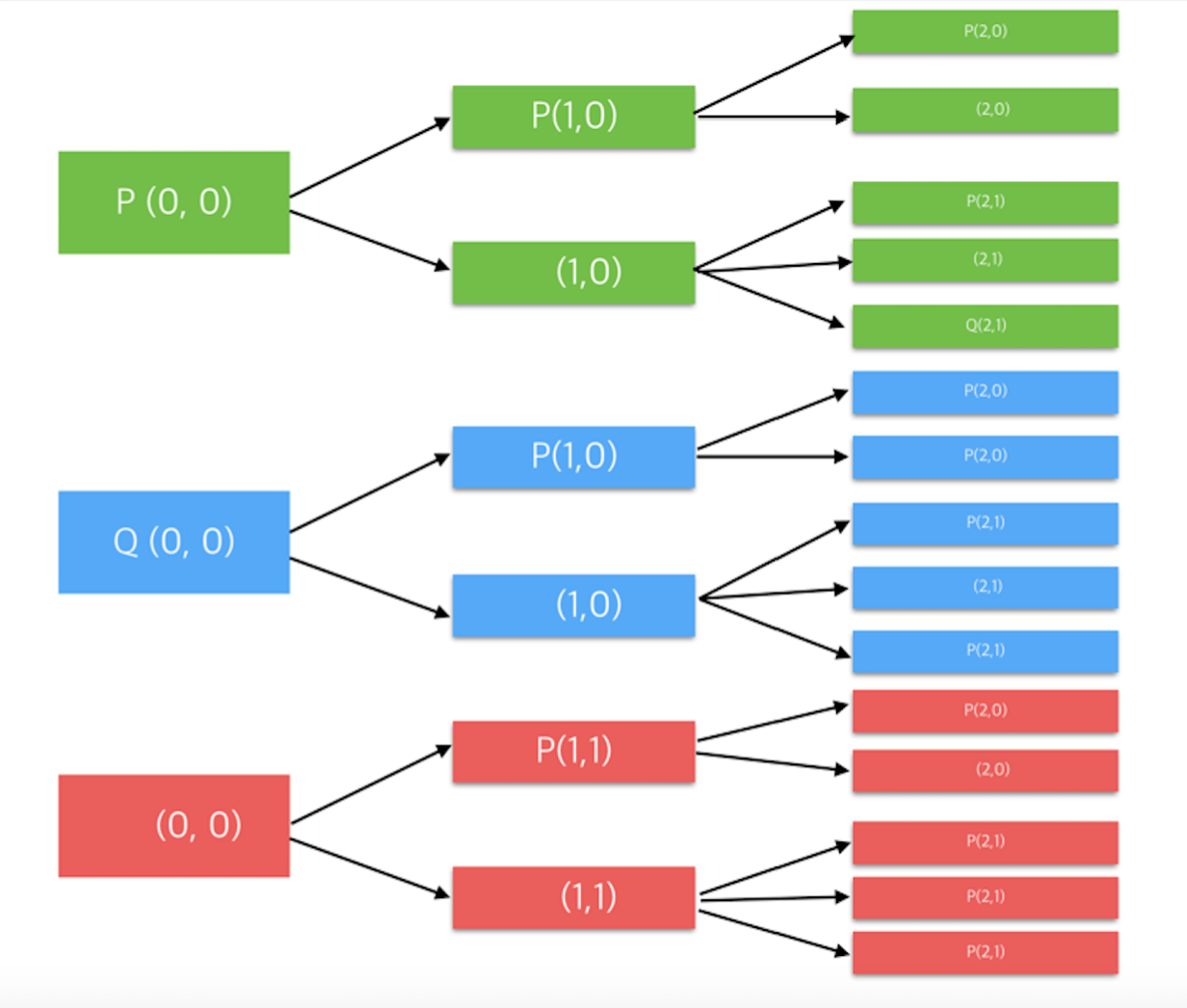
- 선택은 총 3가지로 나눌 수 있다.
  1. P사 업무 선택 후 다음 주의 재귀함수 호출
  2. Q사 업무 선택을 위해 이번 주 쉬고 다음 주의 재귀함수 호출
  3. 이 전 주에서 Q사 업무를 선택하라고 해서 Q사 업무 선택 후 그 다음 주 재귀함수 호출
- 따라서 재귀함수 인자로 현재 주를 의미하는 index 변수와 이 전 주에서 Q사를 선택하라고 지시하는 변수를 받는다.
- 현재 주가 주어진 총 날을 초과하면 0을 반환한다.

3. Implementation

//
//  main.cpp
//  Freelancer
//
//  Created by  Heejun Lee on 7/31/17.
//  Copyright © 2017  Heejun Lee. All rights reserved.
//

#include <iostream>
#include <cstring>

using namespace std;

int T, N;
int P[10000], Q[10000];
int cache[10001][2];

//  (현재 주, 이전 선택)
int scheduler(int week, int pre){   // pre: 0(P), 1(Q)
    int &ret = cache[week][pre];;
    if(ret != -1){
        return ret;
    }
    if(week >= N) return 0;

    int pay = 0;
    // P 선택, Q 선택,
    if(week==0) pay = Q[week] + scheduler(week+1, 0);
    pay = max(pay, P[week] + scheduler(week+1, 0));
    pay = max(pay, scheduler(week+1, 1));

    if(pre == 1)
        pay = max(pay, Q[week] + scheduler(week+1, 0));

    return ret = pay;
}


int main( ) {
    cin >> T;
    for(int t=1;t<=T;t++) {
        memset(P, 0, sizeof(P));
        memset(Q, 0, sizeof(Q));
        memset(cache, -1, sizeof(cache));
        cin >> N;
        int a;
        for(int i=0;i<N;i++){
            cin >> a;
            P[i] = a;
        }
        for(int i=0;i<N;i++){
            cin >> a;
            Q[i] = a;
        }
        cout << "Case #" << t <<endl;
        cout << scheduler(0, 0) << endl;
    }
    return 0;
}

scheduler( ) 함수에서 pre가 1일 때, 즉 Q[week]을 선택해야 할 때 처리해주는 부분을 보자.
- pre가 1이면 사실 P사의 일을 선택하는 일이나, 다음 주 Q사의 일을 위해 넘겨주는 행위는 하지 않고 바로 현재 Q사의 일을 선택해도 된다. 또 어쩌면 이게 더 코드를 최적화한 것처럼 보인다.
- 아래와 같은 코드를 scheduler상단에 위치시켜 불필요한 연산을 하지 않고 바로 반환하는 것이다.
  if(pre == 1) return ret = max(pay, Q[week] + >scheduler(week+1, 0));
- 그러나 정작 실행시켜보면 위의 경우가 시간이 더 오래 걸린다.
- 그 이유는 Feedback에서 알아보자

4. Other Approach

점화식 사용

우선 1주차 dp는 a[1] 또는 b[1]
2주차 dp는 a[1] + a[2] 또는 b[1] + a[2] 또는 b[2] 중 최대값
따라서 dp[i] = max(dp[i-2] + b[i], dp[i - 1] + a[i]) 로 정리할 수 있다.

5. Implementation

#include <iostream>
#include <algorithm>

using namespace std;

int T, N;
int a[10002];
int b[10002];
int dp[10002];

int main()
{
    cin >> T;

    for (int tc = 1; tc <= T; tc++)
    {
        cin >> N;

        memset(a, 0, sizeof(a));
        memset(b, 0, sizeof(b));
        memset(dp, 0, sizeof(dp));

        for (int i = 1; i <= N; i++)
            cin >> a[i];
        for (int i = 1; i <= N; i++)
            cin >> b[i];

        dp[1] = max(a[1], b[1]);
        dp[2] = max({ a[1] + a[2],b[1] + a[2], b[2] });

        for(int i = 3; i <= N; i++)
            dp[i] = max(dp[i - 2] + b[i], dp[i - 1] + a[i]);

        cout << "Case #" << tc << endl << dp[N] << endl;
    }
    return 0;
}

6. Feedback

동적계획법

동적계획법은 결국 모든 경우의 수를 구한다.
비록 중간에 답이 아닌 자명한 경우가 발생하여 따로 예외처리를 해줘도 다른 경로에서 해당 상태로 다시 한 번 와서 같은 연산을 여러 번 해줄 때가 있다.
따라서 어차피 발생할 수 있는 모든 경우로 접근하기 때문에 위와 같은 특수한 상황이더라도 예외처리를 해주지 않고 전부다 구하는 것이 효율적이다.

점화식

지금껏 구현한 동적계획법은 주어진 문제를 단위문제로 나누어 해결한 뒤 그 다음 단위문제로 재귀적 함수를 통해 진행하는 방식이었다. 하지만 이런 단위문제들 간의 상관관계를 파악하여 점화식으로 나타내면 훨씬 더 간단하게 구현할 수도 있다. 본 문제에 적용한 점화식을 도출하는 방법을 다시 한 번 보고 앞으로의 문제해결에 쓸 수 있도록 해야겠다.